Question

Stacy's lifelong dream is to meet Lady Gaga in person. After seeing her

in concert, she IS 100% certain this
dream will come true, but for every year that she does not see her live in concert, she
is half as sure that it will
really happen. Come up with a function that describes the yearly decay of Stacy's lifelong dream.
Let t = the number of years that have passed without her seeing Lady Gaga in concert and D = the percent
of certainty that her dream will come true.

Answer 1

`N(t)=N_(0)((1)/(2))^(t)`

1) The model that fulfills this description is the one that resembles the exponential model "half-life"

2) So we can write out the following considering that year after year her hopes go half:

`\begin{gathered} N(t)=N_0((1)/(2))^t \\ Testing: \\ N(0)=100((1)/(2))^0\Rightarrow N(0)=100 \\ N(1)=100((1)/(2))^1\Rightarrow N(1)=50 \\ N(2)=100((1)/(2))^2\Rightarrow N(2)=25 \end{gathered}`

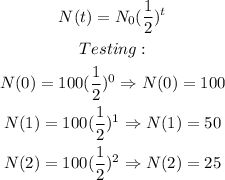
Note that when we test, we can see the number decreasing to half it was in the last year.