Question

If the value of land in an area is increasing 6 percent a year, how long will it take for property values to double?

Answer 1

It will take 11.9 years for the property value to double.

Explanation:

The value of the land is modeled by the following equation:

`P(t) = P(0)(1+r)^(t)`

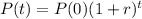
In which P(t) is the value after t years, P(0) is the initial value and r is the growth rate, as a decimal.

In this problem, we have that:

`r = 0.06`

How long will it take for property values to double?

This is t when
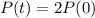`P(t) = 2P(0)`. So

`P(t) = P(0)(1+r)^(t)`

`2P(0) = P(0)(1+0.06)^(t)`

`(1.06)^(t) = 2`

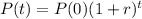
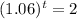
We have that:

`\log{a^(t)} = t\log{a}`

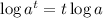
So to find t, we apply log to both sides of the equality.

`\log{(1.06)^(t)} = \log{2}`

`t\log{1.06} = \log{2}`

`t = \frac{\log{2}}{\log{1.06}}`

`t = 11.9`

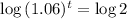
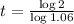
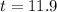
It will take 11.9 years for the property value to double.