we know that
the expression represent the function
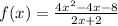
Factor
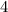 in the numerator
in the numerator
Factor
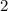 in the denominator
in the denominator
so
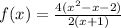
the domain of the function is all real numbers except for
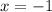 because the denominator can not be zero
because the denominator can not be zero
Simplify the function
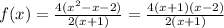
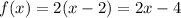
Remember that for
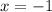 the function does not exist
the function does not exist
so
find the value of f(x) for
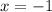 in the simplified function
in the simplified function
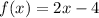
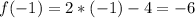
The function has a discontinuity at point
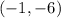
therefore
the answer is the option
graph of 2 x minus 4, with discontinuity at negative 1, negative 6