Question

The graph below shows two functions: function f of x is a straight line which joins the ordered pairs negative 3.5, 15 and 4, 0. Function g of x is a curved line which joins the ordered pairs negative 1.7, 11.5 and 4, 0 Based on the graph, what are the approximate solutions to the equation −2x + 8 = (0.25)x?

A. 8 and 4
B. 1 and 4
C. -1.7 and 4
D. 1.7 and -4

Answer 1

-1.7 and 4

Explanation:

Given Functions:

`y = -2x+8`

`y = 0.25^x`

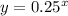
Now to find the the approximate solution we need to find the intersection point of these graph using desmos

Refer the attached figure

So, the intersection points are:

(-1.7,11.57) and (3.998,0.004).

So, the approximate solutions to the equation
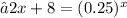`−2x + 8 = (0.25)^x` is -1.7 and 4

Hence Option C is correct

Answer 2

The answer is option C.

Explanation:

when we plot the graph of the function f and function g we obtain that the two graphs meet at two points: (-1.7,12) and (4,0).

so the approximate solution of the equation -2 x+8=(0.25) x are the x-coordinates of the intersecting points which is -1.7 and 4.

Hence the correct option is option C.