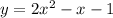Question

Formulate the quadratic function that contains the points (-1,2), (0,-1) and (2,5).

Answer 1

The idea here is to take all three of those points and sub them into the general form of the quadratic equation and solve 3 equations by doing them 2 at a time. The general form is y = ax^2 + bx + c. If we set up the first two equations together using the x and y coordinates of the first 2 coordinates given, the system looks like this: 2 = a(-1)^2 + b(-1) + c
-1 = a(0)^2 +b(0) + c
Solving the second one gives you that c = -1, so we already know c. Solving the first equation we get 2 = a - b - 1, or 3 = a - b, subbing in a -1 for c. The next equation, using the last coordinate, looks like this: 5 = a(2)^2 + b(2) - 1 and
5 = 4a + 2b - 1 and 6 = 4a + 2b. Now we have these two equations left:
3 = a - b and 6 = 4a + 2b. Solve the first equation for b to get it in terms of a only: b = a - 3. Now sub in that b value for b in the second equation:
6 = 4a + 2(a - 3) and 6 = 6a - 6 and 12 = 6a so a = 2. Now we have a and c. Sub in the a value of 2 into b = a - 3 to get 3 = 2 - b. Solve for b to get that b = -1. So our equation in the end finally is y = 2x^2 - x - 1.

Answer 2

The required quadratic function that contain the points is

`y=2x^2-x-1`

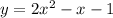
Explanation:

Given : Points (-1,2), (0,-1) and (2,5).

To find : Formulate the quadratic function that contains the points ?

Solution :

The quadratic equation is in the form

`y=ax^2+bx+c`

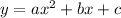
Substituting all the points and then solve the equation form.

Put (-1,2) i.e. x=-1 and y=2

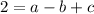`2=a-b+c` ......(1)

Put (0,-1) i.e. x=0 and y=-1

`-1=c` ......(2)

Put (2,5) i.e. x=2 and y=5

`5=4a+2b+c` ......(3)

Substitute the value of c in equation (1) and (3),

We get,

In equation (1),

`2=a-b-1`

`a-b=3` ......(4)

In equation (3),

`5=4a+2b-1`

`4a+2b=6`

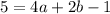
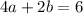
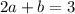`2a+b=3` ......(5)

Solving equation (4) and (5),

Add both equations,

`a-b+2a+b=3+3`

`3a=6`

`a=2`

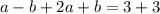
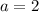
Substitute in equation (4),

`2-b=3`

`b=-1`

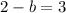
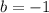
So, we get a=2 , b=-1 and c=-1

Substitute all in general formula of quadratic equation,

`y=ax^2+bx+c`

`y=2x^2-x-1`

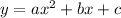
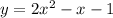
Therefore, The required quadratic function that contain the points is
`y=2x^2-x-1`