Question

What is the radius of a circle whose equation is x² + y² + 8x – 6y + 21 = 0?

__?__ units

Answer 1

(x+4)^2 + (y-3)^2 = 4

Which means, radius is 2, center is (-4,3)

Answer 2

The radius of circle whose equation is
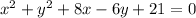`x^2+y^2+8x-6y+21=0` is 2 units.

Explanation:

Given equation of a circle is
`x^2+y^2+8x-6y+21=0`

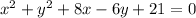
We have to find the radius of the circle whose equation is given.

Consider the given equation of a circle is
`x^2+y^2+8x-6y+21=0`

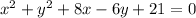
General equation of circle having center at (h,k) with radius r is given as ,

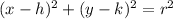`(x-h)^2+(y-k)^2=r^2` ........(1)

we first write the given equation in the general form by making perfect squares,

We know
`(a-b)^2=a^2+b^2-2ab`

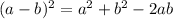
For making perfect square of x, we have terms,
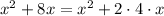`x^2+8x=x^2+2\cdot 4 \cdot x` we just need
`b^2`

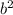
On comparing w have b = 4 , thus
`b^2=16`

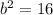
So adding both side 16 , equation becomes,

`x^2+y^2+8x-6y+21+16=16`

`\Rightarrow (x-(-4))^2+y^2-6y+21=16`

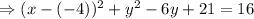
For making perfect square of y, we have terms,
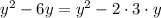`y^2-6y=y^2-2\cdot 3 \cdot y` we just need
`b^2`

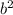
On comparing w have b = 3 , thus
`b^2=9`

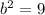
So adding both side 9 , above equation becomes,

`\Rightarrow (x-(-4))^2+y^2-6y+21+9=16+9`

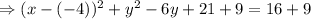
On solving, we get,

`\Rightarrow (x-(-4))^2+(y-3)^2+21=25`

`\Rightarrow (x-(-4))^2+(y-3)^2=25-21`

`\Rightarrow (x-(-4))^2+(y-3)^2=4`

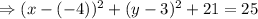
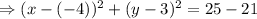
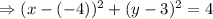
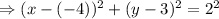`\Rightarrow (x-(-4))^2+(y-3)^2=2^2` .....(2)

Comparing (1) and (2) , we have r= 2

Thus, the radius of circle whose equation is
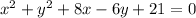`x^2+y^2+8x-6y+21=0` is 2 units.