Question

Find the range and standard deviation of the set of numbers.38, 47, 43, 44, 44, 41, 44The range is 9.The standard deviation is__(Round to the nearest tenth as needed.)

Answer 1

To find the standard deviation of this set of numbers, we will use the formula

`s=\sqrt{\frac{\sum_^(x-\text{ }x_(mean))^2\text{ }}{n-1}}`

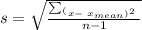
let us explain the parts of this formula, as follows:

`x_(mean)\text{ is the mean of the data \lparen we have to calculate\rparen}`
`n\text{ is the total quantity of numbers \lparen in this example 7\rparen}`

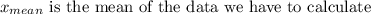
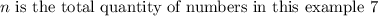
We will proceed by parts, the first thing to do is find the mean of the data

Calculating the mean

To find the mean, we will sum all the numbers and divide by the total quantity of numbers, as follows:

`x_(mean)=(\Sigma x)/(n)=(38+47+43+44+44+41+44)/(7)=(301)/(7)=43`

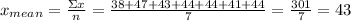
That is, the mean of the set is 43. Now we proceed to find the difference between the data and the mean, and the add them to the power of two, in symbols we have:

`\begin{gathered} \Sigma(x-x_(mean))^2=(38-43)^2+(47-43)^2+(43-43)^2+3*\text{ }(44-43)^2+(41-43)^2 \\ \text{ =\lparen-5\rparen}^2+4^2+0^2+3*\text{ }1^2+(-2)^2 \\ =25+16+3+4 \\ =48 \end{gathered}`

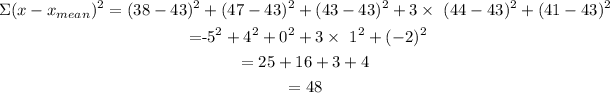
Now we introduce this result into the formula for the standard deviation, we find:

`s=\sqrt{(\Sigma(x-x_(mean))^2)/(n-1)}=\sqrt{(48)/(7-1)}=\sqrt{(48)/(6)}=√(8)\approx\text{ 2.8}`

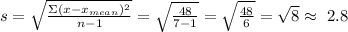
That is, after approximate to the nearest tenth, we found that the standard deviation of the set of numbers is 2.8