Hello! First, let's write some important information contained in the exercise:
committee = 6 students
class: 28 students:
- 10 males
- 18 females
Let's consider the rule: At least three females must be on the committee, so we have some cases, look:
_F_ * _F_ * _F_ * __ * __ * __
1st option:
3 females and 3 males
_F_ * _F_ * _F_ * _M_ * _M_ * _M_
2nd option:
4 females and 2 males
_F_ * _F_ * _F_ * _F_ * _M_ * _M_
3rd option:
5 females and 1 male
_F_ * _F_ * _F_ * _F_ * _F_ * _M_
4th option:
6 females and 0 male
_F_ * _F_ * _F_ * _F_ * _F_ * _F_
Now, we have to use the formula below and find the number of possible combinations:
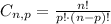
Let's calculate each option below:
1st:
3 females:
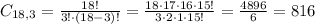
3 males:
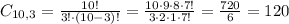
3 females and 3 males: 816 * 120 = 97920
2nd option:
4 females:
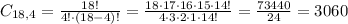
2 males:
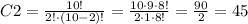
4 females and 2 males: 3060* 45 = 137700
3rd option:
5 females:
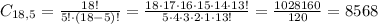
1 male:
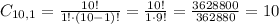
5 females and 1 male = 8568 * 10 = 85680
4th option:
6 females and 0 male:
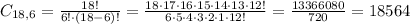
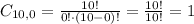
6 females and 0 male: 18564 * 1 = 18564
To finish the exercise, we have to sum the four options:
97920 + 137700 + 85680 + 18564 = 339864
So, right answer A: 339864.