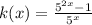Answer:
The required result is
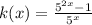
Explanation:
Given : You have two exponential functions. One function has the formula
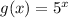 . The other function has the formula
. The other function has the formula
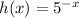 .
.
To find : Which gives formula for
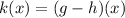 ?
?
Solution :
Let
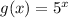 ....(1)
....(1)
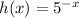 .....(2)
.....(2)
We have to find,
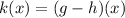
We can write it as,
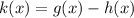 ......(3)
......(3)
Now, substitute the values from (1) and (2) in equation (3),
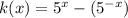
Open the parenthesis on right hand side of equation, we get
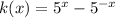
Now, Using
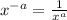
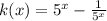
Taking LCM,
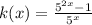
Therefore, The required result is