Question

A block of mass 3 kg slides down an inclined plane inclined at 30° with respect to horizontal. The frictional force between the block and the plane is 8.7 N and the length of the plane is 1 m. What is the work done by the net force when the block reaches the bottom of the plane?

Answer 1

There is positive and negative work being done here.  Negative work is when the force and displacement are in opposite directions (antiparallel vectors).  Since the box moves downhill, following that component of gravity, gravity does positive work, friction (always) does negative work on the object.

Answer 2

The work done by the net force when the block reaches the bottom of the plane is 6 J.

Step-by-step explanation:

Given that,

Mass = 3 kg

Angle = 30°

Frictional force = 8.7 N

Length = 1 m

We need to calculate the work done

The work done is the product of net force and displacement.

Using formula of work done

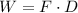`W = F\cdot D`....(I)

We need to calculate the net force

`F_(n)=mg\sin\theta-f_(\mu)`

`F_(n)=3*9.8*\sin30^(\circ)-8.7`

`F_(n)=6\ N`

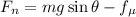
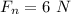
Put the value of net force in equation (I)

`W=6*1`

`W=6\ J`

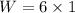
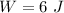
Hence, The work done by the net force when the block reaches the bottom of the plane is 6 J.