Question

The given line passes through the points (0, −3) and (2, 3). What is the equation, in point-slope form, of the line that is parallel to the given line and passes through the point (−1, −1)? y + 1 = ____(x + 1)

Answer 1

Answer: y + 1 = 3 ( x + 1 )

Explanation:

Since, the slope intercept form of a line that is passes through a point
`(x_1, y_1)` and having slope m is,

`y-y_1 = m(x-x_1)`

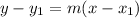
Also, if the line is passes through two points
`(x_1, y_1)` and
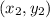`(x_2, y_2)` then the slope of the line is,

`m = (y_2-y_1)/(x_2-x_1)`

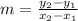
Since, the slope of the line passes through the points (0,-3) and (2,3) is,

`m = (3-(-3))/(2-0)`

⇒
`m = (3+3)/(2)`

⇒
`m = (6)/(2)`

⇒
`m = 3`

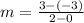
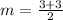
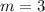
Since, the slope of the line which is parallel to the line passes through the points (0,-3) and (2,3) is,

m = 3

Also, This line is passing through the point (-1,-1)

Therefore, the equation of the line,

y - (-1) = 3(x-(-1))

⇒ y + 1 = 3(x+3)

Answer 2

Note:
If a straight line passes through the points (x1, y1) and (x2, y2), its slope is
m = (y2 - y1)/(x2 -x1).

The given line passes through the points (0, -3) and (2, 3).
Calculate its slope.
m = [3 - (-3)]/[2 - 0] = 6/2 = 3.

Note:
If a straight line has slope = m, and it passes through the point (x1, y1) the equation for the line in point-slope form is
y - y1 = m(x - x1).

A line parallel to the given line will have the same slope of 3.
It passes through the point (-1, -1).

In point-slope form, the parallel line is
y - (-1) = 3(x - (-1))
y + 1 = 3(x+1)

Answer: y + 1 = 3(x+1)