Question

I got disconnected from my tutor, can't reconnect. need an explanation ​

Answer 1

The absolute value function |x| always returns a non-negative number. It takes any number x and returns x if it's already non-negative, or -x if it is negative in order to make it positive.

`|x|=\begin{cases}x&\text{for }x\ge0\\-x&\text{for }x<0\end{cases}`

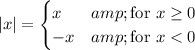
For the equation

-3 + 4 |2x - 5| = 14

rearrange terms to get

|2x - 5| = 17/4

Now,

• if 2x - 5 ≥ 0, then |2x - 5| = 2x - 5. Then

2x - 5 = 17/4

• and if instead 2x - 5 < 0, then |2x - 5| = -(2x - 5), so that

-(2x - 5) = 17/4, or

2x - 5 = -17/4

In the first case,

2x - 5 = 17/4

2x = 17/4 + 5 = 37/4

x = 37/8

In the second case,

2x - 5 = -17/4

2x = -17/4 + 5 = 3/4

x = 3/8