Answer:
Explanation:
Alright, lets get started.
Lets find the volume of cylinder :
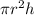
volume of cylinder =
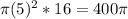
Lets find the volume of cone :
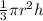
volume of cone =
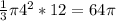
Hence the volume of air space will be volume of cylinder subtracted by volume of cone.
Hence the volume of air space =
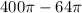
Hence the volume of air space =
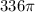
Plugging the value of π as 3.14
volume of air space =
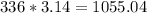 : Answer
: Answer
Hope it will help :)