Question

The function f(x)=2^x and g(x)= f(x+k). If k =-5, what can be concluded about the graph of g(x)?

Answer 1

The graph of
`g(x)` is the graph of
`f(x)` shifted 5 units right.

Answer 2

The graph of g(x) is the graph of f(x) shifted 5 units right.

Explanation:

Horizontal shift:

The parent function y = f(x), then the transformation y = f(x+h) is horizontal shift either right or left.

If h < 0, then the shift is right by h units

if h >0 then, the shift is left by h units

If a parent function

Given the function

`f(x) = 2^x`

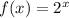
and

`g(x) = f(x+k)`

⇒
`g(x) =2^(x+k)`

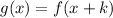
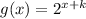
If k = -5 then;

`g(x) = 2^(x-5)`

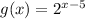
By definition :

k = -5 < 0

⇒the graph of g(x) is the graph of f(x) shifted 5 units right.