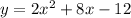Question

Type the correct answer in each box. Use numerals instead of words. If necessary, use / for the fraction bar(s). The vertex of a parabola is (-2, -20), and its y-intercept is (0, -12). The equation of the parabola is y =__x^2 +

__ x +__.

Answer 1

Answer:
`y = 2 x^2 + 8x - 12`

Explanation:

Since the equation of parabola along x-axis is,

`y = a(x-h)^2 + k`

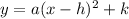
Where (h,k) is the vertex of the parabola and a is any point.

Here, The vertex of a parabola is (-2, -20),

Therefore the equation of parabola is,

`y = a(x+2)^2 -20`

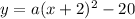
Since, y-intercept is (0, -12),

Therefore, (0,-12) will satisfy the equation of the parabola,

By putting x=0 and y=-12 in the equation of parabola,

`-12 = a(0+2)^2 -20`

⇒
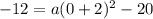
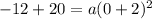`-12 + 20 = a(0+2)^2` ( by adding 12 on both sides )

⇒ 8 = 4 a

⇒ a = 2 ( dividing by 4 on both sides )

Thus, the complete equation of parabola is,

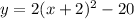
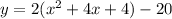
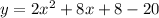
`y = 2(x+2)^2 - 20`

⇒
`y = 2 (x^2+4x + 4) - 20`

⇒
`y = 2x^2 + 8x +8 - 20`

⇒
`y = 2x^2 + 8x - 12`