Question

In triangle ABC, segment BQ is a median of the triangle and point M is the centroid. If BM = 9x and MQ is 5x − 1, what are the values of x and BQ?

Answer 1

1. Draw a figure as the one attached.

2. Point M, the centroid, is the intersection point of the medians.

3. One of the most important properties of M is that it divides any of the medians, in the ratio 2:1, where the larger, is the segment from M to the Vertices.

4. So BM:MQ= 2:1


`(9x)/(5x-1)= (2)/(1)`

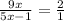
9x=2(5x-1)
9x=10x-2
x=2 (units)

BQ=BM+MQ=9*2+(5*2-1)=18+10-1=28-1=27 (units)