Question

The vertex form of the equation of a parabola is y = 2(x + 3)2 - 5. What is the standard form of the equation?

A) y=2x^2+12x+13

B) y=2x^2+5x+9

C) y=4x^2+4x+4

D) y=2y^2+5y+9

Answer 1

hello :
y = 2(x + 3)² - 5
y = 2(x²+6x+9) -5
y = 2x² +12x +13...(answer : A) y=2x^2+12x+13 )

Answer 2

Option (a) is correct.

The standard form the equation
`y=2(x+3)^2-5` is
`y=2x^2+12x+13`

Explanation:

Given : the vertex form of the equation of a parabola is
`y=2(x+3)^2-5`

We have to write the given equation in standard form and choose the correct from the given options.

Consider the given equation of parabola
`y=2(x+3)^2-5`

The standard form of equation of parabola is
`y=ax^2+bx+c`

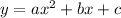
We can obtain the standard form by expanding the square term in the given equation.

Using algebraic identity
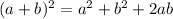`(a+b)^2=a^2+b^2+2ab`, we have,

`\Rightarrow y=2(x+3)^2-5`

`\Rightarrow y=2(x^2+3^2+6x)-5`

Solving brackets, we get,

`\Rightarrow y=2x^2+18+12x-5`

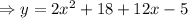
Simplify, we get,

`\Rightarrow y=2x^2+12x+13`

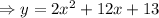
Thus, The standard form the equation
`y=2(x+3)^2-5` is
`y=2x^2+12x+13`