The area of a rectangle is computed as follows:
A = length*height
In this case, the area is 54 ft², then:
54 = xy
Applying the Pythagorean theorem with the height, length, and diagonal of the rectangle we get:
![\begin{gathered} c^2=a^2+b^2 \\ \sqrt[]{117}^2=x^2+y^2 \\ 117^{}=x^2+y^2 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/8gbejkhnklxse4jc375v.png)
Isolating x from the first equation:
54/y = x
Substituting this result into the second equation:
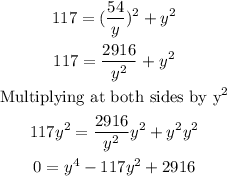
Replacing
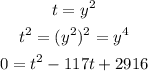
Applying the quadratic formula:
![\begin{gathered} t_(1,2)=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ t_(1,2)=\frac{117\pm\sqrt[]{(-117)^2-4\cdot1\cdot2916}}{2\cdot1} \\ t_(1,2)=\frac{117\pm\sqrt[]{2025}}{2} \\ t_1=(117+45)/(2)=81 \\ t_2=(117-45)/(2)=36 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/40hcv1y3zdq3ugoyr92j.png)
Therefore, in terms of the original variable, y, the solutions are:
![\begin{gathered} y^2_{}=t \\ y=\sqrt[]{t_1}=\sqrt[]{81}=\pm9 \\ y=\sqrt[]{t_2}=\sqrt[]{36}=\pm6 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/xjnyip96yhqnzdcti98e.png)
The negative results have no sense in this case, then the length and width are 9 ft and 6 ft, or vice versa.