Question

Match the functions to their x-intercepts.

Functions: A. f(x) = log x - 1
B. f(x) = - (log x - 2)
C. f(x) = log (-x-2)
D. f(x) = - log -(x - 1)

Pairs:
(0,0) <-------> _____
(-3,0) <------> _____
(10,0) <------> _____
(100,0) <----> _____

Answer 1

hello :
Pairs:
(0,0) <-------> ___D__
(-3,0) <------> ___C__
(10,0) <------> _A____
(100,0) <----> _B____

Answer 2

x- intercepts are where the graph crosses the x-axis i,e

substitute y=f(x)=0 to solve for x;

Given the function:

A)

`f(x) = \log x - 1`

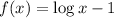
By the definition of x-intercepts;

Substitute y=0 and solve for x;

0 = log x -1

Add 1 to both sides of an equation;

0+1 = log x -1 +1

Simplify:

1 = log x

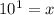`10^1 = x` [Using
`\log_(10) x = b` ⇒
`x =10^b` ]

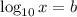Simplify:

x =10

Therefore, x-intercepts is ( 10, 0)

B)

`f(x) =-(\log x - 2)`

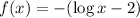
By the definition of x-intercepts;

Substitute y=0 and solve for x;

0 = -(log x - 2) or

log x -2 = 0

Add 2 to both sides of an equation;

log x -2 +2 = 0+2

Simplify:

log x = 2

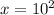`x = 10^2` [Using
`\log_(10) x = b` ⇒
`x =10^b` ]

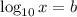Simplify:

x =100

Therefore, x-intercepts is ( 100, 0)

C)

`f(x) =\log (-x -2)`

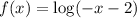
By the definition of x-intercepts;

Substitute y=0 and solve for x;

0 = log (-x - 2) or

log (-x -2) = 0

`-x-2= 10^0` [Using
`\log_(10) x = b` ⇒
`x =10^b` ]

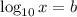Simplify:

-x -2 =1 or

x+2 = -1

subtract 2 from both sides we get

x+2 -2 = -1 -2

Simplify:

x = -3

Therefore, x-intercepts is (-3, 0)

D)

`f(x) =-\log -(x -1)`

By the definition of x-intercepts;

Substitute y=0 and solve for x;

0 = -log -(x - 1) or

log -(x -1) = 0

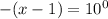`-(x-1)= 10^0` [Using
`\log_(10) x = b` ⇒
`x =10^b` ]

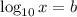Simplify:

-(x -1) =1 or

x - 1 = -1

Add 1 to both sides, we get,

x -1 +1 = -1 +1

Simplify:

x = 0

Therefore, x-intercepts is (0, 0)

Match the function to their intercepts:

(0,0) <-------> __D___

(-3,0) <------> __C___

(10,0) <------> __A___

(100,0) <----> __B___