Question

A study of six hundred adults found that the number of hours they spend on social networking sites each week is normally distributed with a mean of 17 hours. The population standard deviation is 6 hours. What is the margin of error for a 95% confidence interval?

Answer 1

Margin of error = Critical Value × Standard Error

We work out critical value from the information of confidence interval.
We have 95% confidence interval, hence the z-score (that is the critical value) is 1.96 (refer to the picture below)

Standard Error =
`(standard deviation)/( √(sample size) )`
Standard Error =
`(6)/( √(17) ) =1.46`

Margin of error = 1.96 × 1.46 = 2.87 (rounded to 2 decimal place)

Answer 2

Answer: The margin of error for a 95% confidence interval is 0.48.

Explanation:

Since we have given that

N = 600

Mean = 17 hours

Standard deviation = 6 hours

We need to find the margin of error for a 95% confidence interval.

Margin of error is given by

`Error=z* (\sigma)/(√(n))`

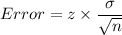
Here, n = 600,
`\sigma=6`

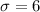
In 95% confidence interval z = 1.96

So, Margin of error would be

`1.96* (6)/(√(600))\\\\=0.48`

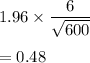
Hence, the margin of error for a 95% confidence interval is 0.48.