Question

Consider the function y=2x2+12x−7.(a) Give the coordinates of the vertex of the graph of the function.(b) Graph the function on a window that includes the vertex

Answer 1

The vertex of a quadratic function can be found in the form

`(h,k)=(-(b)/(2a),f(-(b)/(2a)))`

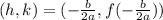
start by finding the h part of the vertex

`\begin{gathered} h=-(12)/(2\cdot2) \\ h=-(12)/(4) \\ h=-3 \end{gathered}`

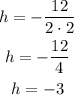
then replace into the function to find k

`\begin{gathered} k=2\cdot(-3)^2+12\cdot(-3)-7 \\ k=2\cdot9-36-7 \\ k=18-36-7 \\ k=-25 \end{gathered}`

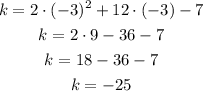
The vertex of the function is (-3-,25)

Then the graph of the function should be an upward parabola since the sign accompanying the a is positive.

For that reason the correct approximate graph is D.