Question

Solve for x. cos(6x) = sin(3x - 9)

Answer 1

Value of x is, 11

Explanation:

Using the trigonometry identity :

`\sin (90-\theta)=\cos \theta`

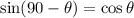
As per the statement:

Solve for x.

`\cos(6x) = \sin(3x - 9)`

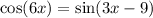
Apply the trigonometry identity we have;

`\sin (90-6x) = \sin (3x-9)`

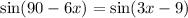
On comparing both sides we have;

`90-6x = 3x-9`

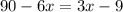
Add 6x to both sides we have;

`90-6x+6x = 3x-9+6x`

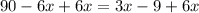
Simplify:

`90= -9+9x`

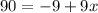
Add 9 from both sides we have;

`99= 9x`

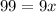
Divide both sides by 9 we have;

11= x

or

x =11

Therefore, the value of x is, 11.