Since

is simultaneously a multiple of 4, 6, and 8, it must be also be a multiple of the least common multiple of the three, which would be 24. So any

, where

is an integer, such that
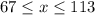
will belong to the desired set of numbers.
The number of positive multiples of 24 less than or equal to 113 is
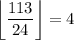
, while the number of positive multiples of 24 less than or equal to 67 is
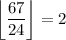
, so there are
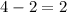
numbers that are each multiples of 4, 6, and 8, and fall between 67 and 113. These numbers are 72 and 96.