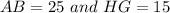we know that
The SSS similarity theorem states that if the ratios comparing the corresponding sides of two triangles are all equal, then the two triangles are similar.
So
in this problem
the corresponding sides are
AB and HG
BC and HI
AC and GI
Step

Find the value of side AB
Applying the Pythagorean Theorem
Step
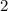
Find the value of side HG
Applying the Pythagorean Theorem
Step
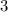
Compare the ratios of the corresponding sides
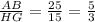
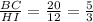
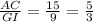
The ratios comparing the corresponding sides of two triangles are all equal, then the two triangles are similar
therefore
the answer is the option