Hello there. To solve this question, we'll have to remember some properties about rotations.
We can solve this question in two different manners. The first is by simply rotating the points, that is, seeing which coordinate it will be after the rotation and labeling the new point as the new vertex of the triangle and the other is by using matrices.
Given the triangle ΔDEF as follows:
To rotate this triangle 180º counterclockwise about the origin (y = 0 or x-axis), we have to reflect this triangle about this axis, by measuring the distance between the points and the axis and marking another three points, at the same distance from the axis, in the opposite direction. Look to the image.
The other way is to use matrices. Suppose in the new coordinates (x', y') of the vertices of the triangle, we'll have the following relation with the former coordinates (x, y):
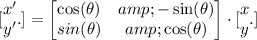
Where the matrix with sines and cosines is called the rotation matrix. Plugging θ = 180º, we get:
By multiplying the matrices, we get:
Therefore we get that all the points now have opposite y coordinates, just as we found before.
By inspection, we find that the coordinates for the triangle ΔDEF were D (1, 1), E (3, 3) and F (6, 1).
The new coordinates will then be given by: