Question

which of the following relationships below represent a function with the greater rate of change than the function y =7/4x +4 ?

Answer 1

The rate of change is given by the slope of the given function, which is the coefficient of the variable x. Then, the given rate of change is

`(7)/(4)`

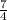
In order to solve this question, we need to find the slope for every case. In general, the slope formula for 2 given points is

`m=(y_2-y_1)/(x_2-x_1)`

Lets start.

Case A.

We can choose 2 points in our table. If we choose

`\begin{gathered} (x_1,y_1)=(4,2) \\ (x_2,y_2)=(8,9) \end{gathered}`

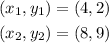
by substituting these points into the slope formula, we get

`\begin{gathered} m=(9-2)/(8-4) \\ m=(7)/(4) \end{gathered}`

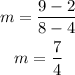
which have the same rate that our given function.

Case B.

If we choose points

`\begin{gathered} (x_1,y_1)=(-4,-2) \\ (x_2,y_2)=(0,3) \end{gathered}`

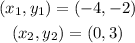
the slope is given by

`\begin{gathered} m=(3-(-2))/(0-(-4)) \\ m=(5)/(4) \end{gathered}`

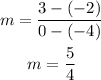
which is less than the given rate of our function

Case C.

If we choose points

`\begin{gathered} (x_1,y_1)=(0,5) \\ (x_2,y_2)=(4,-2) \end{gathered}`

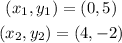
the slope is

`\begin{gathered} m=(-2-5)/(4-0) \\ m=-(7)/(4) \end{gathered}`

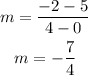
which is less than the given rate of our function because its a negative number.

Case D.

If we choose points

`\begin{gathered} (x_1,y_1)=(-2,-4) \\ (x_2,y_2)=(0,1) \end{gathered}`

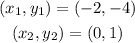
we get

`\begin{gathered} m=(1-(-4))/(0-(-2)) \\ m=(5)/(2) \end{gathered}`

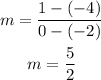
which is greater than the given rate.

Therefore, the answer is option D