Answer:
x = 9.6 meters
y = 20.98 meters
Shadow length = 11.38 meters
Explanation:
By applying tangent rule in right triangle ABD,
tan(21)° =
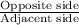
tan(21) =
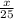
x = 25(tan 21)
x = 9.5966
x ≈ 9.60 meters
Similarly, by applying tangent rule in ΔABC,
tan(40)° =
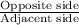
tan(40)° =
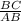
tan(40)° =
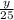
y = 25(tan 40°)
y = 20.98 meters
Length of the shadow of the man = y - x
= 20.98 - 9.60
= 11.38 meters