Question

PLEASE ANSWER QUICKLY I DO NOT NEED AN EXPLANATION JUST THE RIGHT ANSWER

Which equation is the inverse of 5y+4=(x+3)^2+1/2 ?

A. y = 1/5x^2 + 6/5x + 11/10
B. y = 3 +- SR5x+7/2
C. -5y - 4 = -(x+3)^2 - 1/2
D. y = -3 +- SR5x+7/2

"SR" MEANS SQUARE ROOT AND "+-" IS OBVIOUSLY "PLUS OR MINUS"

Answer 1

Answer:
`y=-3+-\sqrt{5x+(7)/(2)}`

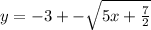
Explanation: Given equation
`5y+4=(x+3)^2+(1)/(2)`.

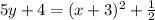We need to find it's inverse.

In order to find the inverse, we need to switch x and y's and solve for y.

Step 1: Switching x and y's, we get

`5x+4=(y+3)^2+(1)/(2)`

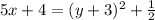
Step 2: Solving it for y.

Subtracting
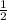`(1)/(2)` from both sides, we get

`5x+4-(1)/(2)=(y+3)^2+(1)/(2)-(1)/(2)`

`5x+4-(1)/(2)=(y+3)^2`

`5x+(8)/(2)-(1)/(2)=(y+3)^2`

`5x+(7)/(2)=(y+3)^2`

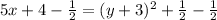
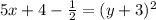
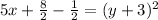
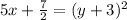
Taking square root on both sides, we get

`\sqrt{5x+(7)/(2)}=√((y+3)^2)`

`\sqrt{5x+(7)/(2)}=y+3`

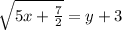
Subtracting 3 from both sides, we get

`\sqrt{5x+(7)/(2)}-3=y`

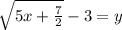
Switching sides, we get

`y=-3+-\sqrt{5x+(7)/(2)}`

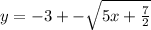
Therefore, correct option is D option
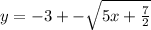`y=-3+-\sqrt{5x+(7)/(2)}`.