The average rate of change is: 4(b + 1)
How to find the average rate of change?
The formula for the average rate of change between the interval (a, b) is:
f'(x) =
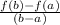
The function is given as:
g(x) = 4x² - 7
Thus, the procedure to find the average rate of change on the interval [1,b] is:
g(1) = 4(1)² - 7
g(1) = -3
g(b) = 4(b)² - 7
g(b) = 4b² - 7
g'(x) = (4b² - 7 - (-3))/(b - 1)
g'(x) = (4b² - 4)/(b - 1)
g'(x) = 4(b + 1)(b - 1)/(b - 1)
g'(x) = 4(b + 1)