Answer:
10 hours
Step-by-step explanation:
The first car drives North at 18mph for 5 hours.
Distance=Speed X Time
Therefore, the distance covered by the first car in x (x>5) hours will be:
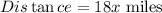
The second car starts driving to the East at 48 mph.
The second car would have been driving for (x-5) hours.
Therefore, the distance covered by the second car in x-5 (x>5) hours will be:
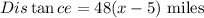
The straight line distance (hypotenuse) between the two at x hours = 300 miles
Applying Pythagoras theorem, we have that:

We solve the equation derived above for x.

We can then solve using the quadratic formula:

Since time cannot be negative
x=10 hours
Therefore, 10 hours after the first car starts driving, the two cars are 300 miles apart.