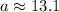Question

which method should I use to solve for the missing side length of the triangle? law of sines, law of cosines, SOH-COH-TOA, or the Pythagorean theorem? solve for the missing side length and round to the nearest tenth! please i am having trouble

Answer 1

5. The Law of Sines states the following:

`(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)`

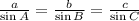
Where the side "a" is opposite angle A, side "b" is opposite angle B and side "c" is opposite angle C.

Given the triangle ABC shown in the exercise, you know the measures of two angles and the length of the side AB, so you can find the missing side length using the Law of Sines.

6. Applying the explained above, you can set up the following equation:

`(8)/(\sin(30\degree))=(a)/(\sin(55\degree))`

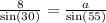
Now you must solve for "a":

`\begin{gathered} \sin (55\degree)\cdot(8)/(\sin(30\degree))=a \\ \\ a\approx13.1 \end{gathered}`

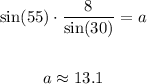
The answers are:

5. First option.

6.

`a\approx13.1`