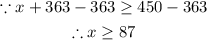Question

Modeling with mathematics Your scores for the first four quizzes are 88, 89, 91, 95. You want to achieve an average of at least 90. What do you need to score on the fifth quiz to achieve your goal? Write an inequality to model this scenario and solve.

Answer 1

The average of the scores = sum/number

The scores are 88, 89, 91, 95

Their sum = 88 + 89 + 91 + 95 = 363

Let the score of the 5th quiz is x

Then the sum of the 5 quizzes = x + 363

Then the average of the 5 quizzes is

`A=(x+363)/(5)`

We need an average of at least 90, then

At least means greater than or equal

`\therefore A\ge90`

Substitute A by its value above

`\therefore(x+363)/(5)\ge90`

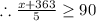
To solve it, multiply both sides by 5 to cancel the denominator on the left side

`\begin{gathered} \because x+363\ge5*90 \\ \therefore x+363\ge450 \end{gathered}`

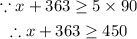
Subtract 363 from both sides to find x

`\begin{gathered} \because x+363-363\ge450-363 \\ \therefore x\ge87 \end{gathered}`