Question

The system of equations below has no solution. 2/3x+5/2y=15 4x+15y=12 Which equation could represent a linear combination of the system? A) 4/3x=42 B)0=26 C)15/2y=33 D)0=0

Answer 1

the answer is B

Explanation:

i got it right on edge 2021

Answer 2

A lnear combination of a system of equations can be obtained by adding/subtracting a multiple of the equations of the of the system.

Given the system of equations

`(2)/(3) x+ (5)/(2) y=15 \ \ \ \ \ \ \ \ (1) \\ \\ 4x+15y=12 \ \ \ \ \ \ \ \ (2)`

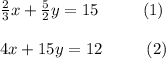
Now multiplying equation (1) by 6 and equation (2) by 1, we have:

`(1)*6\Rightarrow4x+15y=90 \ \ \ \ \ \ \ \ (3) \\ \\ (2)*1\Rightarrow4x+15y=12 \ \ \ \ \ \ \ \ (4)`

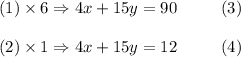
Subtracting equation (4) from equation (3) gives:

`0=78`

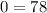
Therefore, a system of linear equation that has no solution results on two unequal numbers in both sides of the equation.
Therefore, the equation that could represent a linear combination of the system is 0 = 26.