Answer:
The distance between the points is approximately 6.4
Explanation:
The given coordinates of the points are;
(2, -2), and (6, 3)
The distance between two points, 'A', and 'B', on the coordinate plane given their coordinates, (x₁, y₁), and (x₂, y₂) can be found using following formula;
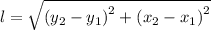
Substituting the known 'x', and 'y', values for the coordinates of the points, we have;
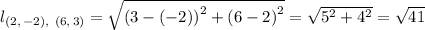
Therefore, the distance between the points, (2, -2), and (6, 3) = √(41) ≈ 6.4.