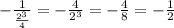Tenemos que determinar si es verdadero o falso.
i) Si x e y son números racionales, entonces x+y también es un número racional. VERDADERO.
j) Si x e y son números irracionales, entonces x+y también es un número irracional. VERDADERO.
k) Para todo x perteneciente a N, existe un y perteneciente a N tal que x+y=0. FALSO: N representa al conjunto de los números naturales (0, 1, 2, 3...). Por ejemplo, para x=1, y debería tener un valor y=-1, pero entonces y no pertenece a los números naturales, por lo que no cumpliría con la premisa.
l) La ecuación x^2+1=0 tiene solución en los reales. FALSO. La solución es x=raíz cuadrada de (-1), que es la definición de i, el número complejo o imaginario. Esta solución no pertenece al conjunto de los números reales.
m) El número 0.3333... es un entero. FALSO. El número no pertenece a los enteros porque no es un número natural ni su opuesto. Este número si se puede expresar como fracción, por lo que pertenece al conjunto de los números reales, pero no es un entero.
n) El inverso de -2^2/4 es -1/2. VERDADERO