Question

Can you just write the work because when I read it i don’t fully understand a problem when there is the explanation after every step of the problemfind the Range of f[g(x)] and the g[f(x)]

Answer 1

The given functions are:

`\begin{gathered} f(x)=2x^2-x+1 \\ g(x)=4x+3 \end{gathered}`

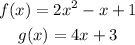
Replace x with g(x) in the expression for the function f(x):

`f(g(x))=2(g(x))^2-g(x)+1`

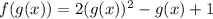
Substitute the equation for g(x) into the equation above:

`\begin{gathered} f(g(x))=2(4x+3)^2-(4x+3)+1_{} \\ \Rightarrow f(g(x))=2(16x^2+24x+9)-4x-3+1 \\ \Rightarrow f(g(x))=32x^2+48x+18-4x-3+1 \\ \Rightarrow f(g(x))=32x^2+48x-4x+18-3+1 \\ \Rightarrow f(g(x))=32x^2+44x+16 \end{gathered}`

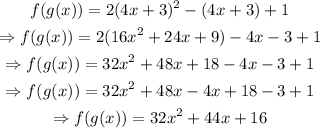
Notice that the composite function f(g(x)) is a quadratic equation.

To find the range of a quadratic equation, you have to find the maximum or the minimum value of the function.

The maximum or minimum point of a quadratic function is the y-coordinate of the vertex.

Note that if the coefficient of x² is positive, then the function has a minimum, but if the coefficient is negative, then the function has a maximum.

In this case, the function has a positive coefficient of x², hence, it has a minimum.

The x-coordinate of the vertex of a quadratic function f(x)=ax²+bx+c is given as:

`x=-(b)/(2a)`

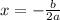
Substitute b=44 and a=32 into the equation:

`x=-(44)/(2(32))=-(11)/(16)`

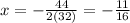
Substitute x=-11/16 into the composite function to get the y-coordinate of the vertex:

`y=32(-(11)/(16))^2+44(-(11)/(16))+16=(7)/(8)`

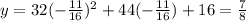
Hence, since the function has a minimum as stated, the range will be all real numbers that are greater or equal to 7/8:

`Range\colon\lbrack(7)/(8),\infty)`

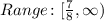
Find the function g(f(x)) using the same procedure:

`\begin{gathered} g(x)=4x+3 \\ \text{Replace x with f(x):} \\ g(f(x))=4(f(x))+3 \\ \Rightarrow g(f(x))=4(2x^2-x+1)+3 \\ \Rightarrow g(f(x))=8x^2-4x+4+3 \\ \Rightarrow g(f(x))=8x^2-4x+7 \end{gathered}`

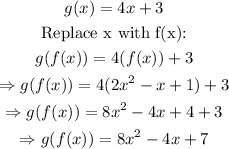
Since

Since