Question

The altitude of an equilateral triangle is 6 units long. The length of one side of the triangle is ____ units.

Answer 1

Given:

height of the equilateral triangle = 6 units

Required:

Length of the side of an equilateral triangle.

Solution:

To solve the problem, we need to split the equilateral triangle into half. Know that the sum of all the angles in a triangle is 180°. Since, we know that each angle in a equilateral triangle is 60°, splitting it into half gives us a 30-60-90 triangle.
The length of each side of a 30-60-90 triangle is as follows:
1. The side opposite to the angle 30° is equal to x/2.
2. The side opposite to the angle 60°, which is the altitude, is square root of 3 divided by 2.
3. The side opposite to the angle 90°, which is the length of the side is equal to x.

Since we know the value of the altitude, we can equate its corresponding equation.

x√3/2 = 6
x = 6.9 units or approximately 7 units.

Answer 2

The length of one side of the triangle is 4√3 units.

Explanation:

If the length of sides is a units then the altitude of an equilateral triangle is

`h=(√(3))/(2)a`

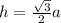
Let the length of one side of the triangle be x units.

`h=(√(3))/(2)x`

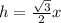
It is given that the altitude of an equilateral triangle is 6 units long.

`6=(√(3))/(2)x`

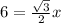
Multiply both sides by 2.

`12=√(3)x`

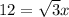
Divide both sides by √3.

`(12)/(√(3))=x`

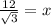
Rationalize the denominator.

`(12)/(√(3))* (√(3))/(√(3))=x`

`(12√(3))/(3)=x`

`4√(3)=x`

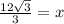
The length of one side of the triangle is 4√3 units.

`x=4√(3)\approx 6.9282`

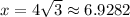
It can be written as 6.9282 units.