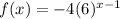Question

Which formula can be used to describe the sequence?

, −4, −24, −144,...

f(x) = 6
f(x) = −6
f(x) = (6)x − 1
f(x) = (−6)x − 1

Answer 1

The formula that can be used to describe the given sequence is
`f(x)=-4(6)^(x-1)`

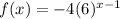
Explanation:

Given : sequence -4, −24, −144,...

We have to find the formula that can be used to describe the given sequence -4, −24, −144,...

A geometric sequence is a sequence in which each higher term is multiplied by a constant number called common ratio.

Written as a, ar , ar², ar³., ....

and general term is calculated as
`a_n=ar^(n-1)`

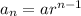
Where a is first term and r is common ratio.

Consider the given sequence -4, −24, −144,...

We find the common ratio ,

`a=-4, \\\\ar=-24,\\\\\ ar^2=-144`

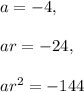
Thus, common ratio is given as
`r=(ar)/(r)=(-24)/(-4)=6`

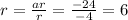
Thus, the given sequence is a geometric sequence.

The general term is given by
`a_n=ar^(n-1)`

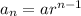
Put a = -4 , r = 6

We have

`a_n=-4(6)^(n-1)`

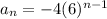
Thus, the formula that can be used to describe the given sequence is
`f(x)=-4(6)^(x-1)`

Answer 2

`f(x) = -4(6)^(x-1)`

Explanation:

Given sequence,

-4, -24, -144, .....

Since,

`(-24)/(-4)=(-144)/(-24)=.........=6`

Thus, the given sequence is the Geometric sequence having common ratio 6,

Since, the formula of nth term of a GP is,

`a_n = ar^(n-1)`

Here, a = -4 ( first term ) and r = 6 ( common difference,

Let x represents the total number of terms,

And, f(x) represents the xth term,

Then the required formula would be,

`f(x) = -4(6)^(x-1)`