Question

[tex]in cos(3x)+1, why isn't The "Period" =pi/3?

Shift should be "0", I hope.
What's the range?[/tex]

Answer 1

Let the period be
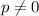
`p\\eq0`. Then by definition, a
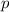
`p`-periodic function
`f(x)` satisfies


`f(x)=f(x+p)`

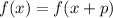
where here
`f(x)=\cos3x`.


`\cos3x=\cos3(x+p)=\cos(3x+3p)`

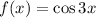
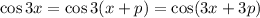
We know that
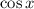
`\cos x` is
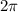
`2\pi`-periodic, i.e.


`\cos x=\cos(x+2\pi)`

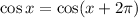
which reveals that we should also have


`\cos3x=\cos(3x+2\pi)`

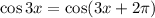
and so
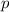
`p` is such that
`3p=2\pi\implies p=\frac{2\pi}3`.

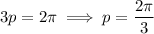
In general, the period of
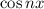
`\cos nx` is
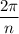
`\frac{2\pi}n`. (The same applies for
`\sin nx`.)

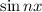
The range can be found by recalling that
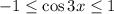
`-1\le\cos3x\le1`, which means
`0\le\cos3x+1\le2`.