Question

Find the limit of the function by using direct substitution. limit as x approaches two of quantity x squared plus eight x minus two.

Answer 1

`\displaystyle \lim_(x\to 2)x^2+8x-2=2^2+8\cdot2-2=4+16-2=18`

Answer 2

Answer: The limit of the given function as x approaches 2 is 18.

Step-by-step explanation: We are given to find the limit of the following function by using direct substitution.

"limit as x approaches two of quantity x squared plus eight x minus two".

The given function can be written as

`f(x)=x^2+8x-2.`

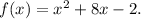
Since we are to find the value of the limit by direct substitution, so we get

`L\\\\=\lim_(x\rightarrow 2)f(x)\\\\=\lim_(x\rightarrow 2)(x^2+8x-2)\\\\=2^2+8* 2-2\\\\=4+16-2\\\\=18.`

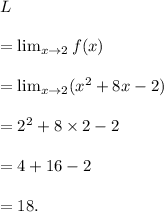
Thus, the limit of the given function as x approaches 2 is 18.