Question

What are the number of integral solutions of the equation 2x+2y+z=20 such that x>=0 , y>=0 , z>=0?

Answer 1

`2x+2y+z=20\\ z=(20)/(2x+2y)\\ z=(10)/(x+y)`

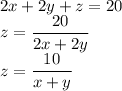
Now, for z to be an integer, the sum x+y must be a divisor of 10.
It has to be a positive divisor since z≥0. Also x≠y.


`x+y=1 \\ x=1-y\\`
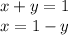
x≥0 and y≥0 so y can be equal to either 0 or 1. There are 2 solution in this case.


`x+y=2\\ x=2-y\\`
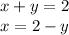
In this case, y can be equal to 0,1, or 2, but for y=1 ⇒ x=1, so there are two solutions.


`x+y=5\\ x=5-y`
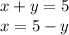
y can be 0,1,2,3,4 or 5 - 6 solutions


`x+y=10\\ x=10-y`
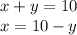
y can be 0,1,2,3,4,5,6,7,8,9,10, but for y=5 ⇒ x=5, so 10 solutions.

2+2+6+10=20 solutions in total.