Answer: The correct answer is 209.12 km/h.
Step-by-step explanation:
The expression for the average velocity is as follows;
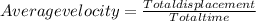
It is given in the problem that an airplane travels to the south at 968 km/h for 2.50 hours. The same airplane lands, and then takes off again, turning north and traveling at 875 km/h for 1.75 hours.
Calculate the total time taken by airplane.
t= 2.50 h+ 1.75 h
t= 4.25 h
Calculate the distance when an airplane travels to the south.
d'= st
Here, s is the speed and t is the time taken
Put s= 968 km/h and t= 2.50 h.
d'= (968)(2.50)
d'= 2420 km
Calculate the distance when an airplane travels to the north.
d''= st
Here, s is the speed and t is the time taken
Put s= 875 km/h and t= 1.75 h.
d''= (875)(1.75)
d''= 1531.25 km
Calculate the total displacement.
d= d'-d''
Put d'= 2420 km and d''= 1531.25 km.
d= (2420)- (1531.25)
d= 888.75 km
Calculate the the average velocity of the airplane.
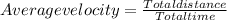
Put Total displacement, d= 888.75 km and t= 4.25 h
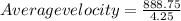
Average velocity= 209.12 km/h
Therefore, the airplane's average velocity for this trip is 209.12 km/h.