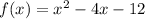
x-intercpets: value of x when f(x)=0. Use the quadratic formula:
![\begin{gathered} x^2-4x-12=0 \\ \\ x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \\ x=\frac{-(-4)\pm\sqrt[]{(-4)^2-4(1)(-12)}}{2(1)} \\ \\ x=\frac{4\pm\sqrt[]{64}}{2} \\ \\ x=(4\pm8)/(2) \\ \\ x_1=(4+8)/(2)=6 \\ \\ x_2=(4-8)/(2)=-2 \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/l4blik39r7bsqu2uxu5e.png)
X-intercept: (6,0) and (-2,0)
y-intercept: value of f(x) when x=0:
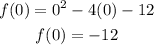
Y-intercept: (0, -12)
Vertex: use the next foruma to find the x value in vertex:
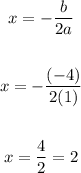
Use that value of x to find the coordinate in y for the vertex:
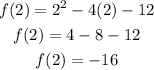
Vertex: (2, -16)
Axis of symmetry: value of x in the vertex.
Axis of simmetry: x=2
Maximim or minimum: if in the quadratic equation, the coefficient of the square x is possitive the parabola opens up and has a minimun value. If the coefficient of the square x is negative the parabola opens down and and has a maximum value.
Minimum
The minimum value is in the vertex (2 ,-16) is the value of the function f(x) in the vertex (the value of coordinate y):
Min value: -16Graph: