Answer:
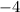 Graph of parent function is shifted to right by 4 units.
Graph of parent function is shifted to right by 4 units.
Step-by-step explanation:
We have been given a parent function
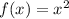 and another function
and another function
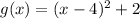 . We are asked to determine the horizontal translation from the graph of the parent function to the graph of the function g(x).
. We are asked to determine the horizontal translation from the graph of the parent function to the graph of the function g(x).
Let us recall translation rules.
Horizontal translation:
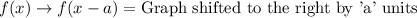
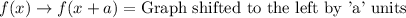
Vertical translation:
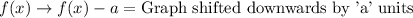
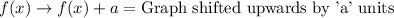
Upon comparing our functions, we can see that parent function is shifted to right by 4 units and upwards by 2 units to get the the function g(x).
Therefore, the value horizontal translation is
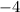 , which indicates the graph is shifted to right by 4 units.
, which indicates the graph is shifted to right by 4 units.