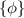Question

What is the solution set of the quadratic inequality 6x2 + 1 <_ 0

Answer 1

Answer :
`x^2\leq -1/6`

Step-by-step explanation:

`6x^2 +1 \leq 0`

shifting 1 to Right hand side becomes -1

`6x^2\leq -1`

shifting 6 on right hand side will divide -1 becomes -1/6

`x^2\leq -1/6`

Quadratic equation is the equation having degree 2 and inequality which is not equal to right hand side

Answer 2

No solution.

The solution set is
`\left \{ \phi \right \}`

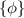
Step-by-step explanation:

We have been given the quadratic inequality
`6x^2+1\leq 0`

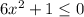
Subtract 1 to both sides

`6x^2+1-1\le \:0-1\\\\6x^2\le \:-1`

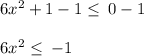
Divide both sides by 6

`(6x^2)/(6)\le (-1)/(6)\\\\x^2\le \:-(1)/(6)`

Now, we know that square of a number always gives positive values.

Thus, the above result never hold true for any real values of x.

Therefore, the inequality has no solution.

Hence, the solution set is
`\left \{ \phi \right \}`