Question

"The front row of a stadium has 25 seats. Each of the other rows has two more seats than the row in front of it. How many seats are there altogether in the first 20 rows?" (I need to use a formula related to arithmetic sequences to solve this problem.)

Answer 1

880 seats

Explanations:

To get the total sum of seats in the first 20 rows, you will use the formula for finding the sum of the nth term of an arithmetic sequence as shown:

`S_n=(n)/(2)\lbrack2a+(n-1)d\rbrack`

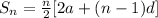
where

• a is the, first term

,

• n is the, number of terms

,

• d is the, common difference

If the front row of a stadium has 25 seats and each of the other rows has two more seats than the row in front of it, then the sequence formed by this statement is;

25, 27, 29...

From the sequence:

• a = 25

,

• d = 27 - 25 = 29 - 27 = 2

,

• n = 20 (sum of the first 20 rows)

Substitute the given parameters into the formula:

`\begin{gathered} S_(20)=(20)/(2)\lbrack2(25)+(20-1)\cdot2\rbrack \\ S_(20)=10\lbrack50+2(19)\rbrack \\ S_(20)=10(50+38) \\ S_(20)=10(88) \\ S_(20)=880 \end{gathered}`

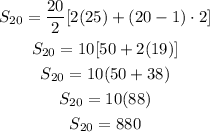
Therefore the number of seats that are there altogether in the first 20 rows is 880 seats