Question

Graph the line of the equation using its slope and y-intercept y= -2/3x+3

Answer 1

Given: The equation below

`y=-(2)/(3)x+3`

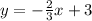
To Determine: The graph representing the equation using the slope and y-intercept

Solution

Step 1: Determine the y-intercept

To calculate the y-intercept, make x = 0

`\begin{gathered} y=-(2)/(3)x+3,x=0 \\ y=-(2)/(3)(0)+3 \\ y=0+3 \\ y=3 \end{gathered}`

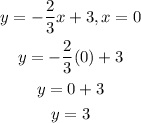
The coordinate of the y-intercept is (0, 3)

Step 2: Determine the x-intercept

To calculate the x-intercept, make y = 0

`\begin{gathered} y=-(2)/(3)x+3,y=0 \\ 0=-(2)/(3)x+3 \\ (2)/(3)x=3 \\ 2x=3*3 \\ 2x=9 \\ x=(9)/(2) \\ x=4.5 \end{gathered}`

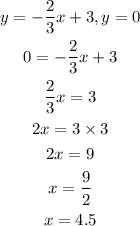
The coordinate of the x-intercept is (4.5, 0)

Step 3: Determine the slope

The general equation of a straight line is given as

`\begin{gathered} y=mx+c \\ m=\text{slope} \\ c=y-\text{ intercept} \end{gathered}`

Compare the general equation to the given equation

`\begin{gathered} y=-(2)/(3)x+3 \\ y=mx+c \\ slope(m)=-(2)/(3) \end{gathered}`

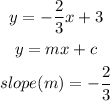
Use the coordinates of y-axis, x-axis and the slope to plot graph as shown below