Question

Rounded to the nearest tenth, what is the area of rectangle ABCD?

Answer 1

Given the rectangle ABCD, you can identify that it is divided into two Right Triangles:

`\begin{gathered} \Delta ACD \\ \Delta ABD \end{gathered}`

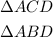
• You can find the length of the rectangle by applying the following Trigonometric Function:

`\cos \alpha=(adjacent)/(hypotenuse)`

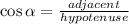
In this case, you can set up that:

`\begin{gathered} \alpha=30\degree \\ adjacent=CD=AB=l \\ hypotenuse=AD=9 \end{gathered}`

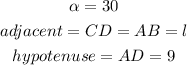
Then, substituting values and solving for "l", you get:

`\begin{gathered} \cos (30\text{\degree})=(l)/(9) \\ \\ 9\cdot\cos (30\text{\degree})=l \\ \\ l=(9)/(2)\sqrt[]{3}ft \end{gathered}`

• In order to find the width of the rectangle, you can use this Trigonometric Function:

`\sin \alpha=(opposite)/(hypotenuse)`

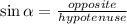
In this case, you can say that:

`\begin{gathered} \alpha=30\degree \\ opposite=AC=BD=w \\ hypotenuse=AD=9 \end{gathered}`

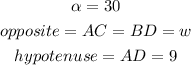
Therefore, substituting values and solving for "w", you get:

`\begin{gathered} \sin (30\degree)=(w)/(9) \\ \\ 9\cdot\sin (30\degree)=w \\ \\ w=(9)/(2)ft \end{gathered}`

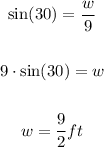
• Now you need to use the following formula for calculating the area of a rectangle:

`A=lw`

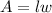
Where "l" is the length and "w" is the width.

Substituting the length and the width of the given rectangle into the formula and evaluating, you get:

`A=((9)/(2)\sqrt[]{3}ft)((9)/(2)ft)`
`A\approx35.1ft^2`

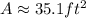
Hence, the answer is: Option C.