Question

n(1+10n)-n(4n-3) how do I use the distributive property and combine like terms to simplify? I dont understand why it has to be rearranged to n(10n+1)-n(4n-3) before.

Answer 1

For this problem, we need to use the distributive property to simplify the following expression:

`n(1+10n)-n(4n-3)`

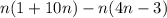
The distributive property states that if we have a number multiplying a sum, we need to find the sum of the products. We don't need to change the order of "1+10n", but it won't interfere with the results, as "1+10n" is equal to "10n+1".

The expression below shows the application of the distributive property:

`n\cdot1+n\cdot10n-n\cdot4n-n\cdot(-3)`

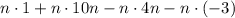
Now we need to calculate all the individual products, which is done below:

`\begin{gathered} n+10n^2-4n^2+3n \\ 10n^2-4n^2+n+3n \end{gathered}`

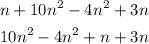
All the terms with equal literal parts were arranged to be close together, since the literal part is equal, we can add or subtract the numeric part, and conserve the literal one. This is done below:

`6n^2+4n`

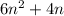
The simplified expression is equal to 6n²+4n.