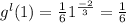Answer:
D)
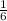
g¹(1) =
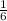
The inverse of the function
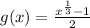
Explanation:
Step(i):-
Given that f(x) = (2x+1)³
Let y = (2x+1)³
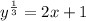
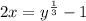
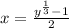
Step(ii):-
y = f(x) ⇒ x = f⁻¹ (y)
⇒
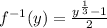
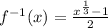
The inverse of the given function
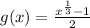
Differentiating equation (i) with respective to 'x', we get
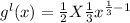
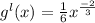
Final answer:-
Put x=1